Time Limit Airsoft Free for All

Time Limit Airsoft Free for All

Summary

Learn how to compare algorithms and develop code that scales! In this postal service, we cover eight Big-O notations and provide an instance or 2 for each. We are going to learn the top algorithm's running time that every developer should be familiar with. Knowing these time complexities will help you to assess if your code volition scale. Also, it'south handy to compare multiple solutions for the same problem. Past the terminate of it, you would be able to eyeball dissimilar implementations and know which ane volition perform better without running the code!

In the previous mail, nosotros saw how Alan Turing saved millions of lives with an optimized algorithm. In most cases, faster algorithms can salvage you time, coin and enable new engineering science. And so, this is paramount to know how to mensurate algorithms' performance.

What is time complexity?

To recap time complication estimates how an algorithm performs regardless of the kind of automobile information technology runs on. You can go the time complexity past "counting" the number of operations performed by your code. This time complexity is defined as a part of the input size n using Large-O notation. due north indicates the input size, while O is the worst-case scenario growth charge per unit role.

Nosotros employ the Big-O annotation to classify algorithms based on their running time or infinite (retentivity used) every bit the input grows. The O function is the growth charge per unit in function of the input size n.

Here are the big O cheatsheet and examples that we will cover in this mail before nosotros swoop in. Click on them to go to the implementation. 😉

Big O Annotation	Proper noun	Example(south)
O(1)	Constant	# Odd or Even number, # Await-up table (on boilerplate)
O(log n)	Logarithmic	# Finding chemical element on sorted array with binary search
O(due north)	Linear	# Find max element in unsorted array, # Duplicate elements in array with Hash Map
O(northward log n)	Linearithmic	# Sorting elements in array with merge sort
O(n2)	Quadratic	# Indistinguishable elements in array **(naïve)**, # Sorting array with chimera sort
O(northward3)	Cubic	# 3 variables equation solver
O(iin)	Exponential	# Find all subsets
O(n!)	Factorial	# Detect all permutations of a given set/string

Now, Let's go i by one and provide lawmaking examples!

You can find all these implementations and more in the Github repo: https://github.com/amejiarosario/dsa.js

---

This post is part of a tutorial series:

Learning Data Structures and Algorithms (DSA) for Beginners

1. Intro to algorithm's time complication and Large O note

2. 8 time complexities that every developer should know 👈 you lot are here

3. Information Structures for Beginners: Arrays, HashMaps, and Lists

4. Graph Data Structures for Beginners

5. Trees Data Structures for Beginners

6. Self-counterbalanced Binary Search Trees

7. Appendix I: Analysis of Recursive Algorithms

---

O(1) - Constant fourth dimension

O(i) describes algorithms that take the same amount of time to compute regardless of the input size.

For instance, if a function takes the aforementioned time to process ten elements and 1 meg items, so we say that information technology has a constant growth charge per unit or O(1). Let's see some cases.

Examples of abiding runtime algorithms:

• Observe if a number is even or odd.
• Cheque if an item on an assortment is null.
• Impress the first element from a list.
• Find a value on a map.

For our give-and-take, we are going to implement the first and last case.

Odd or Even

Find if a number is odd or even.

1 2 3 four 5 6

office isEvenOrOdd(n) { return north % 2 ? 'Odd' : 'Even'; } console.log(isEvenOrOdd(x)); console.log(isEvenOrOdd(10001));

Advanced Annotation: you could also supervene upon northward % 2 with the bit AND operator: n & i . If the first fleck (LSB) is 1 then is odd otherwise is even.

It doesn't thing if n is x or 10,001. It will execute line two 1 time.

Practise non be fooled past one-liners. They don't always translate to abiding times. You accept to be aware of how they are implemented.

If you have a method like Array.sort() or whatsoever other array or object method, you have to look into the implementation to determine its running time.

Archaic operations similar sum, multiplication, subtraction, segmentation, modulo, bit shift, etc., have a constant runtime. Did you look that? Let's become into detail about why they are constant fourth dimension. If yous use the schoolbook long multiplication algorithm, it would take O(north2) to multiply two numbers. However, virtually programming languages limit numbers to max value (e.g. in JS: Number.MAX_VALUE is 1.7976931348623157e+308). So, y'all cannot operate numbers that yield a upshot greater than the MAX_VALUE. So, primitive operations are bound to exist completed on a fixed corporeality of instructions O(one) or throw overflow errors (in JS, Infinity keyword).

This example was piece of cake. Permit'south do another ane.

Wait-upwardly tabular array

Given a string, observe its word frequency data.

1 2 iii 4 five 6 7 8

const dictionary = {the: 22038615, exist: 12545825, and: 10741073, of: 10343885, a: 10144200, in: 6996437, to: 6332195 }; part getWordFrequency(dictionary, word) { return dictionary[word]; } panel.log(getWordFrequency(dictionary, 'the')); console.log(getWordFrequency(dictionary, 'in'));

Again, we can be certain that even if the dictionary has 10 or one one thousand thousand words, it would withal execute line 4 once to find the word. Still, if nosotros decided to store the dictionary as an array rather than a hash map, it would exist a different story. In the next section, we will explore what's the running time to find an detail in an array.

Merely a hash tabular array with a perfect hash role volition take a worst-example runtime of O(1). The ideal hash part is not practical, then some collisions and workarounds atomic number 82 to a worst-case runtime of O(north). Still, on average, the lookup fourth dimension is O(1).

O(n) - Linear fourth dimension

Linear running time algorithms are widespread. These algorithms imply that the program visits every chemical element from the input.

Linear fourth dimension complication O(n) means that the algorithms take proportionally longer to consummate every bit the input grows.

Examples of linear time algorithms:

• Get the max/min value in an assortment.
• Find a given element in a drove.
• Impress all the values in a listing.

Permit'southward implement the first instance.

The largest item on an unsorted array

Permit's say you want to find the maximum value from an unsorted array.

1 2 3 4 v vi 7 8 9 10 11 12 13 14

function findMax(due north) { allow max; let counter = 0; for (permit i = 0; i < n.length; i++) { counter++; if(max === undefined || max < n[i]) { max = n[i]; } } console.log(`n: ${n.length}, counter: ${counter}`); return max; }

How many operations will the findMax role exercise?

Well, information technology checks every element from n. If the electric current item is more than meaning than max it volition do an assignment.

Find that we added a counter to count how many times the inner block is executed.

If you get the fourth dimension complication, it would be something like this:

• Line 2-3: 2 operations
• Line iv: a loop of size n
• Line half dozen-8: three operations inside the for-loop.

And so, this gets usa 3(n) + 2.

Applying the Big O note that we learn in the previous postal service, we merely need the biggest order term, thus O(n).

We tin verify this using our counter. If n has iii elements:

ane 2

findMax([3, i, 2]);

or if north has nine elements:

1 2	findMax([iv,5,6,1,9,2,8,3,seven])

At present imagine that you accept an array of 1 million items. Do yous call up it volition have the aforementioned time? Of course not. It will take longer to the size of the input. If we plot n and findMax running fourth dimension, we volition have a linear function graph.

O(n^2) - Quadratic fourth dimension

A function with a quadratic time complexity has a growth rate of n². If the input is size 2, it volition practice four operations. If the input is size 8, it will take 64, and so on.

Here are some examples of quadratic algorithms:

• Check if a collection has duplicated values.
• Sorting items in a collection using bubble sort, insertion sort, or selection sort.
• Observe all possible ordered pairs in an array.

Let's implement the first 2.

Has duplicates

You want to find duplicate words in an assortment. A naïve solution will be the following:

i two 3 4 5 6 7 8 ix ten 11 12 thirteen fourteen 15 16 17 18 19

function hasDuplicates(n) { const duplicates = []; let counter = 0; for (allow outter = 0; outter < northward.length; outter++) { for (let inner = 0; inner < north.length; inner++) { counter++; if(outter === inner) keep; if(north[outter] === north[inner]) { render true; } } } console.log(`n: ${n.length}, counter: ${counter}`); return simulated; }

Time complexity analysis:

• Line 2-3: ii operations
• Line 5-half dozen: double-loop of size northward, and so n^2.
• Line 7-xiii: has ~iii operations within the double-loop

We get 3n^2 + 2.

When we take an asymptotic analysis, nosotros drop all constants and exit the nearly critical term: n^2. And then, in the big O notation, information technology would exist O(north^two).

We are using a counter variable to assist usa verify. The hasDuplicates role has two loops. If we have an input of 4 words, it will execute the inner block 16 times. If we accept 9, it will perform counter 81 times and so forth.

i 2	hasDuplicates([1,2,3,4]);

and with n size nine:

1 2	hasDuplicates([1,two,three,iv,5,6,7,8,9]);

Permit's see another example.

Bubble sort

Nosotros want to sort the elements in an array. One way to practise this is using bubble sort as follows:

1 2 3 4 5 vi seven eight 9 10 11 12 13 14 xv 16 17 18 nineteen

office sort(n) { for (let outer = 0; outer < n.length; outer++) { permit outerElement = northward[outer]; for (let inner = outer + one; inner < n.length; inner++) { permit innerElement = north[inner]; if(outerElement > innerElement) { n[outer] = innerElement; n[inner] = outerElement; outerElement = n[outer]; innerElement = due north[inner]; } } } return north; }

Yous might also notice that for a very big n, the time it takes to solve the problem increases a lot. Can you spot the relationship between nested loops and the running time? When a role has a unmarried loop, information technology usually translates into a running time complication of O(northward). At present, this part has 2 nested loops and quadratic running time: O(n²).

O(n^c) - Polynomial time

Polynomial running is represented as O(n^c), when c > 1. As you already saw, ii inner loops almost translate to O(n²) since it has to get through the array twice in most cases. Are iii nested loops cubic? If each one visit all elements, so aye!

Ordinarily, we want to stay away from polynomial running times (quadratic, cubic, due north^c, etc.) since they take longer to compute every bit the input grows fast. Still, they are not the worst.

Triple nested loops

Let's say yous desire to observe the solutions for a multi-variable equation that looks similar this:

3x + 9y + 8z = 79

This naïve plan volition requite you lot all the solutions that satisfy the equation where 10, y, and z < n.

1 2 3 iv 5 6 vii 8 9 ten 11 12 13 fourteen fifteen 16 17

function findXYZ(n) { const solutions = []; for(let x = 0; x < due north; x++) { for(let y = 0; y < north; y++) { for(let z = 0; z < n; z++) { if( iii*x + 9*y + 8*z === 79 ) { solutions.push({x, y, z}); } } } } render solutions; } console.log(findXYZ(x));

This algorithm has a cubic running time: O(north^3).

** Note:** We could do a more efficient solution to solve multi-variable equations, but this works to show an instance of a cubic runtime.

O(log n) - Logarithmic time

Logarithmic time complexities usually apply to algorithms that divide problems in one-half every time. For instance, let's say that nosotros want to look for a book in a dictionary. As you know, this book has every discussion sorted alphabetically. If you are looking for a give-and-take, then there are at least two means to do it:

Algorithm A:

1. Start on the outset page of the book and become word by word until you find what you are looking for.

Algorithm B:

1. Open the book in the eye and check the showtime give-and-take on it.
2. If the word you lot are looking for is alphabetically more than significant, then look to the right. Otherwise, look in the left half.
3. Carve up the residue in half again, and repeat pace #2 until you lot find the word y'all are looking for.

Which one is faster? The outset algorithms go give-and-take by word O(n), while the algorithm B separate the problem in half on each iteration O(log n). This 2nd algorithm is a binary search.

Binary search

Find the index of an element in a sorted array.

If nosotros implement (Algorithm A) going through all the elements in an array, it volition have a running time of O(n). Can nosotros do better? We can try using the fact that the collection is already sorted. Subsequently, we tin split it in half equally nosotros look for the element in question.

1 2 3 four five half-dozen seven 8 9 ten eleven 12 13 14 15 16 17 18 19 20 21

function indexOf(array, element, outset = 0 ) { const one-half = parseInt(array.length / two); const current = array[half]; if(electric current === element) { return offset + one-half; } else if(element > current) { const right = assortment.slice(half); return indexOf(right, chemical element, offset + half); } else { const left = array.piece(0, one-half) render indexOf(left, element, first); } } const directory = ["Adrian", "Bella", "Charlotte", "Daniel", "Emma", "Hanna", "Isabella", "Jayden", "Kaylee", "Luke", "Mia", "Nora", "Olivia", "Paisley", "Riley", "Thomas", "Wyatt", "Xander", "Zoe"]; console.log(indexOf(directory, 'Hanna')); panel.log(indexOf(directory, 'Adrian')); console.log(indexOf(directory, 'Zoe'));

Computing the time complexity of indexOf is non every bit straightforward as the previous examples. This function is recursive.

In that location are several ways to analyze recursive algorithms. For simplicity, we are going to utilise the Principal Method.

Master Method for recursive algorithms

Finding the runtime of recursive algorithms is non equally easy as counting the operations. This method helps us to determine the runtime of recursive algorithms. We are going to explain this solution using the indexOf function as an illustration.

When analyzing recursive algorithms, we care most these iii things:

• The runtime of the work done exterior the recursion (line three-iv): O(one)
• How many recursive calls the problem is divided (line xi or 14): 1 recursive call. Detect only one or the other will happen, never both.
• How much north is reduced on each recursive call (line x or 13): 1/2. Every recursive call cuts n in half.

1. The Master Method formula is the following:

T(n) = a T(n/b) + f(northward)

where:

• T: time complexity function in terms of the input size northward.
• n: the size of the input. duh? :)
• a: the number of sub-problems. For our case, nosotros only split the problem into one subproblem. So, a=one.
• b: the cistron by which due north is reduced. For our instance, nosotros divide n in half each time. Thus, b=2.
• f(north): the running fourth dimension exterior the recursion. Since dividing past 2 is constant time, we take f(n) = O(1).

2. Once we know the values of a, b and f(due north). Nosotros tin can decide the runtime of the recursion using this formula:

north^log_ba

This value will help us to observe which master method case we are solving.

For binary search, we have:

n^log_ba = n^log_two1 = n₀ = 1

3. Finally, nosotros compare the recursion runtime from step 2) and the runtime f(due north) from stride 1). Based on that, we have the following cases:

Case 1: Most of the piece of work washed in the recursion.

If northlogba > f(n),

then runtime is:

O(north^log_ba)

Example 2: The runtime of the work washed in the recursion and outside is the same

If nlogba === f(northward),

and so runtime is:

O(n^log_ba log(northward))

Case three: Nigh of the work is done outside the recursion

If nlogba < f(northward),

then runtime is:

O(f(n))

At present, let's combine everything we learned here to get the running time of our binary search function indexOf.

Master Method for Binary Search

The binary search algorithm slit n in half until a solution is establish or the array is exhausted. So, using the Master Method:

T(north) = a T(northward/b) + f(n)

1. Find a, b and f(north) and replace information technology in the formula:

• a: the number of sub-problems. For our example, nosotros only split the problem into another subproblem. So a=i.
• b: the cistron by which n is reduced. For our case, we dissever n in half each time. Thus, b=2.
• f(n): the running time exterior the recursion: O(1).

Thus,

T(n) = T(n/two) + O(i)

2. Compare the runtime executed within and outside the recursion:

• Runtime of the piece of work done exterior the recursion: f(north). E.g. O(one).
• Runtime of work done inside the recursion given past this formula nlogba . E.thousand. O(northlog2one ) = O(n0 ) = O(1).

3. Finally, getting the runtime. Based on the comparison of the expressions from the previous steps, detect the case it matches.

As we saw in the previous step, the piece of work outside and inside the recursion has the same runtime, then we are in case two.

O(n^log_ba log(n))

Making the substitution, nosotros get:

O(due north^log_two1 log(due north))

O(n⁰ log(n))

O(log(n)) 👈 this is the running time of a binary search

O(north log due north) - Linearithmic

Linearithmic fourth dimension complexity it'south slightly slower than a linear algorithm. However, it'south still much better than a quadratic algorithm (you will see a graph at the very stop of the post).

Examples of Linearithmic algorithms:

• Efficient sorting algorithms like merge sort, quicksort, and others.

Mergesort

What'southward the best way to sort an array? Before, we proposed a solution using bubble sort that has a time complexity of O(northⁱⁱ). Can we practise better?

We can use an algorithm called mergesort to improve it. This is how mergesort works:

1. We are going to divide the array recursively until the elements are ii or less.
2. We know how to sort two items, so we sort them iteratively (base example).
3. The concluding step is merging: we merge in taking ane past one from each array such that they are in ascending society.

Hither's the lawmaking for merge sort:

1 2 three iv 5 six 7 8 9 10 11 12 13 14 15 sixteen 17 18 nineteen xx 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 forty 41 42 43 44 45 46

office sort(array = []) { const size = assortment.length; if (size < 2) { return assortment; } if (size === 2) { return array[0] > array[1] ? [array[1], array[0]] : assortment; } const mid = parseInt(size / 2, 10); return merge(sort(array.slice(0, mid)), sort(assortment.piece(mid))); } function merge(array1 = [], array2 = []) { const merged = []; permit array1Index = 0; let array2Index = 0; while (array1Index < array1.length || array2Index < array2.length) { if (array1Index >= array1.length || array1[array1Index] > array2[array2Index]) { merged.push(array2[array2Index]); array2Index += ane; } else { merged.push(array1[array1Index]); array1Index += 1; } } return merged; }

As you can see, information technology has two functions, sort and merge. Merge is an auxiliary role that runs once through the collection a and b, and so it'southward running fourth dimension is O(due north). Let's apply the Master Method to find the running time.

Chief Method for Mergesort

We are going to use the Master Method that we explained above to find the runtime:

1. Let'due south observe the values of: T(northward) = a T(northward/b) + f(n)

   • a: The number of sub-issues is two (line 20). Then, a = ii.
   • b: Each of the sub-problems divides n in half. So, b = 2
   • f(n): The work washed outside the recursion is the role merge, which has a runtime of O(n) since it visits all the elements on the given arrays.

Substituting the values:

T(n) = 2 T(north/2) + O(n)

2. Permit's find the work done in the recursion: northlogba .

north^log_iiii

due north¹ = northward

3. Finally, we can see that recursion runtime from step 2) is O(n) and also the non-recursion runtime is O(n). And then, we have the case 2 : O(nlogba log(due north))

O(n^log₂two log(north))

O(nⁱ log(n))

O(due north log(north)) 👈 this is running time of the merge sort

O(2^n) - Exponential time

Exponential (base 2) running time means that the calculations performed by an algorithm double every time as the input grows.

Examples of exponential runtime algorithms:

• Power Gear up: finding all the subsets on a set.
• Fibonacci.
• Travelling salesman problem using dynamic programming.

Power Ready

To empathize the power prepare, permit's imagine you are buying a pizza. The store has many toppings that you tin choose from, similar pepperoni, mushrooms, bacon, and pineapple. Allow's phone call each topping A, B, C, D. What are your choices? Yous tin select no topping (yous are on a diet ;), you can cull one topping, or two or iii or all of them, and so on. The power set gives you all the possibilities (BTW, there 16 with four toppings, as you lot will see later)

Finding all distinct subsets of a given set. For example, let'due south do some examples to try to come up upward with an algorithm to solve it:

1 2 3

powerset('') powerset('a') powerset('ab')

Did yous discover any pattern?

• The first returns an empty element.
• The second case returns the empty element + the 1st element.
• The third case returns precisely the results of the 2d instance + the aforementioned assortment with the 2d element b appended to it.

What if you desire to notice the subsets of abc? Well, it would be precisely the subsets of 'ab' and over again the subsets of ab with c appended at the end of each element.

Every bit you noticed, every time the input gets longer, the output is twice equally long as the previous 1. Let's lawmaking it up:

ane 2 three 4 five vi 7 8 9 10 11 12 13

function powerset(n = '' ) { const array = Assortment.from(northward); const base = ['']; const results = array.reduce((previous, element) => { const previousPlusElement = previous.map( el => { render `${el} ${element}`; }); render previous.concat(previousPlusElement); }, base); render results; }

If we run that function for a couple of cases nosotros will get:

1 2 3 4 5 six seven 8 nine 10 11 12

powerset('') powerset('a') powerset('ab') powerset('abc') powerset('abcd') powerset('abcde')

Every bit expected, if y'all plot n and f(due north), yous will notice that information technology would be exactly like the function 2^n. This algorithm has a running fourth dimension of O(ii^n).

** Annotation:** You should avoid functions with exponential running times (if possible) since they don't scale well. The time it takes to procedure the output doubles with every additional input size. But exponential running time is not the worst yet; others go fifty-fifty slower. Let'due south run into one more than instance in the next section.

O(n!) - Factorial time

Factorial is the multiplication of all positive integer numbers less than itself. For example:

v! = 5 x four 10 three x 2 x 1 = 120

It grows pretty rapidly:

twenty! = 2,432,902,008,176,640,000

As you might guess, you lot want to stay away, if possible, from algorithms that have this running time!

Examples of O(northward!) factorial runtime algorithms:

• Permutations of a cord.
• Solving the traveling salesman problem with a brute-force search

Let's solve the first example.

Permutations

Write a function that computes all the different words that tin can be formed given a string. E.chiliad.

1 2 3

getPermutations('a') getPermutations('ab') getPermutations('abc')

How would you solve that?

A straightforward mode volition be to cheque if the string has a length of 1. If so, return that string since you tin't arrange information technology differently.

For strings with a length bigger than 1, we could employ recursion to divide the problem into smaller problems until nosotros go to the length 1 case. We tin take out the first grapheme and solve the trouble for the remainder of the string until nosotros have a length of 1.

one 2 iii iv 5 6 7 8 ix 10 11

office getPermutations(string, prefix = '' ) { if(string.length <= 1) { return [prefix + string]; } return Array.from(string).reduce((event, char, index) => { const reminder = string.slice(0, alphabetize) + cord.slice(index+one); issue = issue.concat(getPermutations(reminder, prefix + char)); render issue; }, []); }

If print out the output, it would be something similar this:

1 2 3 iv five vi 7 8

getPermutations('ab') getPermutations('abc') getPermutations('abcd') getPermutations('abcde')

I tried with a string with a length of 10. It took around 8 seconds!

ane two 3 4

time node ./lib/permutations.js

I take a little homework for you:

Can y'all attempt with a permutation with 11 characters? ;) Comment below on what happened to your computer!

All running complexities graphs

We explored the most mutual algorithms running times with i or ii examples each! They should requite you an idea of how to summate your running times when developing your projects. Beneath yous can find a nautical chart with a graph of all the time complexities that we covered:

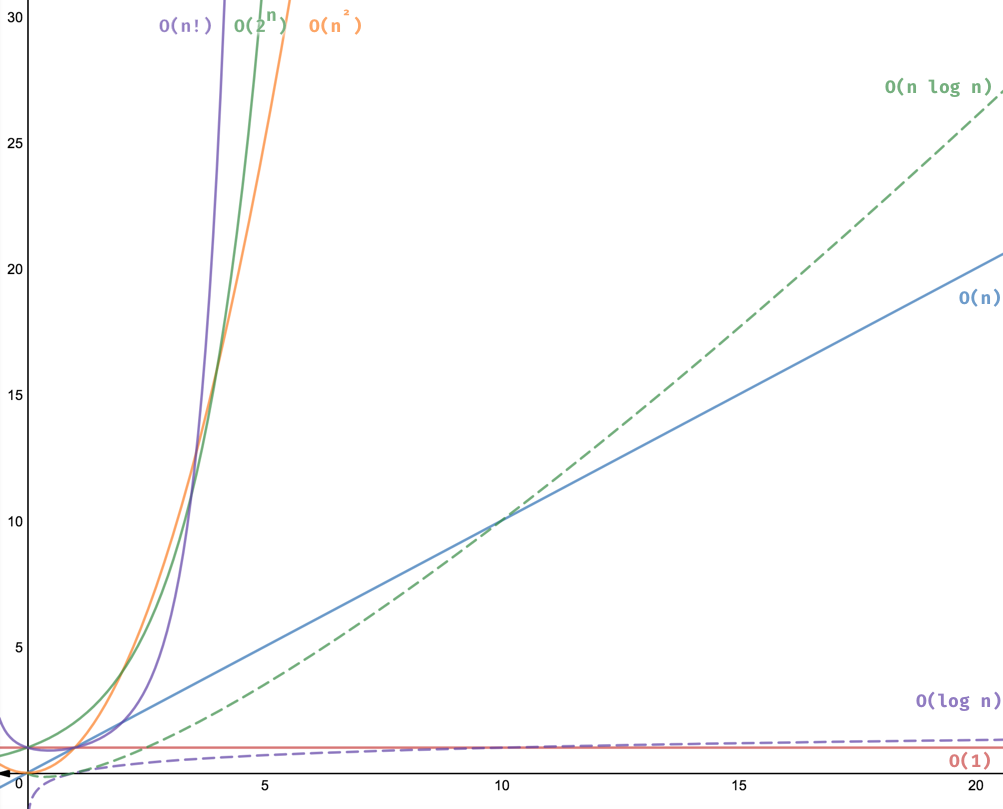
Listen your time complexity!

Time Limit Airsoft Free for All

Posted by: vanhoosedadogiag.blogspot.com

Share this post